INTEGRAL INDEFINIDA

---

La integración es el proceso contrario a la derivación,
El término integración tiene dos acepciones en matemáticas:

1. Dada una función hallar su primitiva, o lo que es lo mismo, dada la derivada de una función, hallar dicha función (integral indefinida).
2. Es una sumatoria de un número infinito de infinitésimos (integral definida).

La integración es conocida como laANTIDERIVACIÓN

ANTIDERIVACIÓN

En cierta forma ya se ha familiarizado con las operaciones inversas. La adición y la sustracción son operaciones inversas, así como la multiplicación y la división, además de la potenciación y la extracción de raíces, la ANTIDERIVACIÓN es lo contrario a la derivación.Una función F se denomina antiderivada de la función f en un intervalo I sí F´(x) = f(x) para todo valor de x en I.
Es el proceso mediante el cual se determina el conjunto de todas las antiderivadas de una función dada.
El símbolo ʃ denota la operación de antiderivación, y se escribe:


ʃ f(x) dx = F(x) + C
INTEGRAL INDEFINIDAEn cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función Fcuya derivada es f, es decir, F ′ = f.
Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 y F2 son dos primitivas de f, entonces existe un número real C, tal queF1 = F2 + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:
El proceso de hallar la primitiva de una función se conoce como integración indefinida, y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.

TEOREMAS PRINCIPALES

• Teorema 1:

Si: f y g son dos funciones definidas en el intervalo I, tales que:
f´(x) = g´(x) para toda x en I entonces existe una constante K tal que:
f (x) = g (x) + K para toda x en I.

• Teorema 2:

Si: F es una antiderivada particular de f en un intervalo I, entonces entonces cada antiderivada de f en I está dada por:

F(x) + C
donde C es una constante arbitraria, y todas las antiderivadas de f en I pueden obtenerse a partir de (1) asignando .valores particulares a C.

Otras propiedades de linealidad de la integral indefinida
La primitiva es lineal, es decir:

1. Si f es una función que admite una primitiva F sobre un intervalo I, entonces para todo real k, una primitiva de kf sobre el intervalo I es kF.
2. Si F y G son primitivas respectivas de dos funciones f y g, entonces una primitiva de f + g es F + G.

La linealidad se puede expresar como sigue:

La primitiva de una función impar es siempre par:En efecto, como se ve en la figura siguiente, las áreas antes y después de cero son opuestas, lo que implica que la integral entre -a y a es nula, lo que se escribe así: F(a) - F(-a) = 0, F siendo una primitiva de f, impar. Por lo tanto siempre tenemos F(-a) = F(a): F es par.

Integral de función impar.png

La primitiva F de una función f par es impar con tal de imponerse F(0) = 0
En efecto, según la figura, la áreas antes y después de cero son iguales, lo que se escribe con la siguiente igualdad de integrales:

Integral de función par.png

Es decir F(0) - F(- a) = F(a) - F(0). Si F(0) = 0, F(- a) = - F(a): F es impar.

La primitiva de una función periódica es la suma de una función lineal y de una función periódica


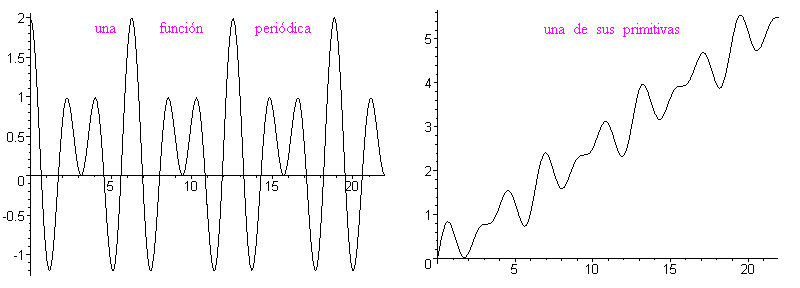
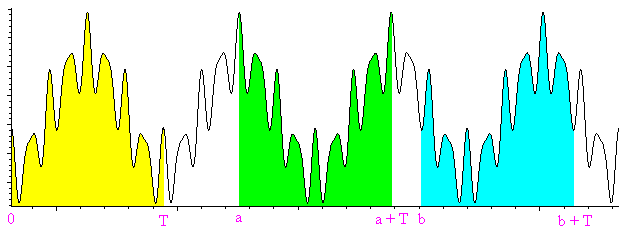
Para probarlo, hay que constatar que el área bajo una curva de una función periódica, entre las abcisas x y x + T (T es el período) es constante es decir no depende de x. La figura siguiente muestra tres áreas iguales. Se puede mostrar utilizando la periodicidad y la relación de Chasles, o sencillamente ¡con unas tijeras! (cortando y superponiendo las áreas de color).
En término de primitiva, significa que F(x + T) - F(x) es una constante, que se puede llamar A. Entonces la función G(x) = F(x) - Ax/T es periódica de período T. En efecto G(x + T) = F(x + T) - A(x + T)/T = F(x) + A - Ax/T - AT/T = F(x) - Ax/T = G(x). Por consiguiente F(x) = G(x) + Ax/T es la suma de G, periódica, y de Ax/T, lineal.

Y por último, una relación entre la integral de una función y la de su recíproca. Para simplificar, se impone f(0) = 0; a es un número cualquiera del dominio de f. Entonces tenemos la relación:

El área morada es la integral de f, el área amarilla es la de f -1, y la suma es el rectángulo cuyos costados miden a y f(a) (valores algebraicos).
Se pasa de la primera curva, la de f, a la segunda, la de f -1 aplicando la simetría axial alrededor de la diagonal y = x.
El interés de esta fórmula es permitir el cálculo de la integral de f -1 sin conocer una primitiva; de hecho, ni hace falta conocer la expresión de la recíproca.

---

CÁLCULOS DE PRIMITIVAS

INTEGRALES INMEDIATAS: Para encontrar una primitiva de una función dada, basta con descomponerla (escribirla bajo forma de una combinación lineal) en funciones elementales cuyas primitivas son conocidas o se pueden obtener leyendo al revés una tabla de derivadas, y luego aplicar la linealidad de la integral:

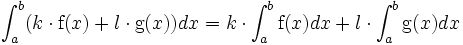
Aquí están las principales funciones primitivas:

Función F ,! : primitiva de f ,!	función f ,! : derivada de F ,!

Por ejemplo, busquemos una primitiva de x → x(2-3x). Como no se conocen primitivas de un producto, desarrollemos la expresión: x(2-3x)= 2x - 3x2. 2x es la derivada de x2, 3x2 es la de x3, por lo tanto 2x - 3x2 tiene como primitiva x2 - x3 + k. Si además se pide que la primitiva verifique una condición F(x0) = y0 (que recibe el nombre de condición inicial cuando se trata de un problema de física), entonces la constante k es unívocamente determinada. En el ejemplo, si se impone F(2) = 3, entonces forzosamente k = 7
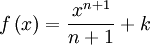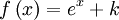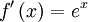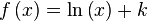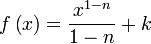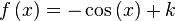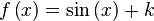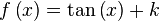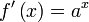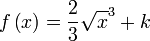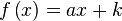2. APLICACIONES DE LA INTEGRAL

2.1 Aplicación en la Física (cinemática):Resumen de los factores que define un movimiento rectilíneo, con las siguientes ecuaciones:

• Posición: X(m) Ec. 1
• Desplazamiento: Xm=X-Xo Ec. 2
• Velocidad media: Vm=V-Vo Ec. 3
• Velocidad: V=dX/dt (m/s) Ec. 4
• Aceleración media: am=V-Vo/t-to (m/s) Ec. 5
• Aceleración: a=d(d(x))/dt(dt) Ec. 6

La aceleración es la ecuación derivada de la posición respecto al tiempo.
Si en las ecuaciones 3 y 5 despejamos dt

dt=dv/a
dt=dx/v
Igualamos las dos ecuaciones y despejamos la aceleración.

a=v(dv)/dx

DETERMINACIÓN DEL MOVIMIENTO RECTILÍNEO DE UNA PARTÍCULA.Un movimiento queda completamente determinado cuando se conoce sus tres ecuaciones horarias:

1. X=f(t)
2. V=f(t) 3. a=f(t)


CASO I:Cuando X=f (t) es conocido.Cuando se conoce la ecuación de la posición en función del tiempo f (t) =XPara hallar la ecuación de la ecuación, se deriva la ecuación de la posición respecto al tiempo.

V=dx/dt
Para hallar la ecuación de la aceleración, se deriva la ecuación de la velocidad respecto al tiempo.

a=dx/dt=d(dx)/dt(dt)


CASO II:Cuando a f (t) es conocido.Para hallar las ecuaciones de la velocidad V= f (t) aplicamos la operación de la inversa de la derivación que es la integración.Partimos de la ecuación a=dv/dt y despejamos dv.
dv=adtdv=f(t)dt
Integramos ambos miembros.


ʃ dv = ʃ f(t)dt
Esta ecuación se define Velocidad en función del tiempo.
A consecuencia de la integración se introduce una constante arbitraria, debido a que hay muchos movimientos que corresponde a al aceleración dada

a= f (t).

Para definir unívocamente el movimiento de la partícula que estamos analizando es necesario especificar las condiciones iníciales del movimiento es decir los valores de X y V para el tiempot=0.
Condiciones iníciales para t=0.

X= Xo posición inicial
V=Vo velocidad inicial
Condiciones iníciales para t=t .
X=X
V=V

Podemos transformar las integrales indefinidas en integrales indefinidas introduciendo como límite inferiores de la integral las condiciones iníciales y como limites superiores las condiciones correspondientes a t=tl.
V = ʃ adt + vo (Ecuación diferencial de la velocidad)
ECUACIÓN DE LA POSICIÓNPartimos de la ecuación.
v=dx/dt
Despejamos dx :
dx=vdt
Integramos ambos miembros
ʃ dx= ʃ vdt + C Transformamos la integral indefinida en integral definida obtenemos la ecuación.
x = ʃ v dt+Xo se sabe que los limites se dan de 0 a t
CASO III:Cuando a = f(t)es conocida
Partimos de la ecuación y despejamos.
a=v(dv)/dtv dv
a dx Sustituimos a por f(x). vdv
f(x) xIntegramos ambos miembros.ʃ vdv = ʃ f(x)dx
APLICACIONES EN EL MOVIMIENTO RECTILÍNEO UNIFORMEMENTE
La velocidad es constante;
V=cte y a=0.
Ecuación de la posición.
x = ʃ vdt+xo
x= v ʃ fdt+xo
x= vt+xo (Ecuación de la posición)

APLICACIONES EN EL MOVIMIENTO RECTILÍNEO UNIFORMEMENTE VARIADO
La aceleración es constante a= cte
Ecuación de la velocidad.
v= ʃ adt+ Vov=a ʃ dt+ Vov=at + Vo (Ecuación de la velocidad)

x= ʃ vdt + xox= ʃ (vo+at)dt + xox= ʃ vodt+ ʃ atdt+ xox=voʃ dt + a ʃ tdt + xox=vot + a t^2/2 + xo (Ecuacion de la posicion)

Ejemplos:

1. Una partícula con movimiento rectilíneo tiene por ecuación de la aceleración a=6t m/s, si en el instante inicial de la observación de la partícula se encuentra en la abscisa -20m con velocidad de -4 m/s. determinar:

• a) las ecuaciones horarias del movimiento
• b) la posición aceleración y velocidad a los 2 s

Solución

• a) Las ecuaciones horarias del movimiento.

a=6tm/s(s)v= ʃadt+vov=6 ʃt(dt)+vov=3t(t)-4x= ʃvdt+xox= ʃ(3t(t)-4)dt-20x=3 ʃt(t)dt-4 ʃdt-20x=t(t)(t)-2t(t)-20

• b) la posición aceleración y velocidad a los 2 s

a=6ta=6(2)a=12m/s(s)v=3t(t)-4v=3(4)-4v=8m/sx=t(t)(t)-2t(t)-20x=8-2(4)-20x=-20m

3. FORMAS DE INTEGRACIÓN

3.1 de Integración Directa:

• ʃ dx = x + C
• ʃ m dx = m x + C (m es una constante)
• ʃ xⁿ dx = xⁿᶧ¹/n+1 + C ; n diferente de -1
• ʃ ( dx+dy+dz ) = ʃ dx + ʃ dy + ʃ dz
• ʃ [ F´(x) / F(x) ] dx = ln |F(x)| + C
• ʃ [ F(x) ]ⁿ [ F´(x) ] dx = [ F(x) ]ⁿᶧ¹ / n+1 + C ; n diferente de -1
• ʃ eᵡ dx = eᵡ + C
• ʃ aᵡ dx = aᵡ / ln a + C

3.2 Integración por sustitución
El método de integración por sustitución o por cambio de variable se basa en realizar un reemplazo de variables adecuado que permita convertir el integrando en algo sencillo con una integral o antiderivada simple. En muchos casos, donde las integrales no son triviales, se puede llevar a una integral de tabla para encontrar fácilmente su primitiva. Este método realiza lo opuesto a la regla de la cadena en la derivación.
Procedimiento práctico
Supongamos que la integral a resolver es:






Ahora necesitamos sustituir también dx para que la integral quede sólo en función de u:
Tenemos que por tanto derivando se obtiene 4xdx= du
Se despeja  se agrega donde corresponde en (1):


Debemos considerar si la sustitución fue útil y por tanto se llegó a una forma mejor, o por el contrario empeoró las cosas. Luego de adquirir práctica en esta operación, se puede realizar mentalmente. En este caso quedó de una manera más sencilla dado que la primitiva del coseno es el seno. Como último paso antes de aplicar la regla de Barrow con la primitiva debemos modificar los límites de integración. Sustituimos x por el límite de integración y obtenemos uno nuevo.



De interés
Supongamos ahora que la integral a resolver es:



Véase el video:



3.3 Integrales de Funciones Trigonométricas:

• ʃ cos x dx = sen x + C
• ʃ sen x dx = - cos x + C
• ʃ sec² x dx = tan x + C
• ʃ csc² x dx = - ctan x + C
• ʃ sec x tan x dx = sec x + C
• ʃ csc x ctan x dx = - csc x + C
• ʃ tan x dx = ln |sec x| + C
• ʃ ctan x dx = ln |sen x| + C
• ʃ sec x dx = ln |sec x + tan x| + C
• ʃ csc x dx = ln |csc x - ctan x| + C

3.4 INTEGRALES DE FORMAS TRIGONOMÉTRICAS :

• Sea "n" un número entero impar

Se basa en la utilización de la identidad trigonométrica fundamental.

sen² θ + cos² =1
sen² θ =1 - cos² θ
cos² θ = 1 - sen² θ

sen² θ=1/2 - 1/2 cos 2θ
cos² θ = 1/2 + 1/2 sen 2θ

Sea "n" sea un número entero positivo
Se basa en la utilización de las identidades trigonométricas:
tan² θ = sec ² θ - 1
cot² θ = csc ² θ - 1

• Sea "n" sea un número entero positivo par

Se basa en la utilización de las identidades trigonométricas:

1 + tan² θ = sec ² θ
1 + cot² θ = csc ² θ


Sea "m" sea un número entero positivo par
Se basa en la identidades trigonométrica
tan² θ = sec ² θ - 1
cot² θ = csc ² θ - 1

Sea "n" sea un número entero positivo impar
Se basa en la utilización de la fórmula de integración por partes:

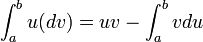int_a^b u (dv) = uv - int_a^b vdu

• 4. INTEGRACION POR PARTES

FORMULA DE INTEGRACION POR PARTES

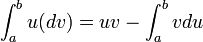
1. Deducción de la formula de recurrencia Matemática
2. Solución de diferenciales que contienen productos especiales de funciones
3. Solución de diferenciales que contienen logaritmos naturales de funciones
4. Solución de diferenciales que contienen funciones trigonométricas inversas
5. Aplicaciones

1. Deducción de Formulas de Recurrencia Matemática

I = ʃ sen ф d ф ; ne {1,2,3,4……}
I = ʃ sen^n-1 ф senф d ф = uv - ʃvdu
u = sen^n-1ф dv = sen ф d ф
du = (n-1)sen^n-2 ф cos ф d ф ʃdv = ʃsen ф d ф
v = - cos ф
I = sen^n-1ф (-cos ф) - ʃ(-cos ф)^(n-1) sen^n-2ф cos ф d ф
I = -sen^n-1ф cos ф + (n-1) ʃsen^n-2 cos2 ф d ф
I = -sen^n-1ф cos ф + (n-1) ʃsen^n-2 ф (1 – sen2ф) d ф
I = -sen^n-1ф cos ф + (n-1) ʃsen^n-2 ф d ф – (n-1) ʃsen^n ф d ф
I + (n-1) I = -sen^n-1ф cos ф + (n-1) ʃsen^n-2 ф d ф
n I = -sen^n-1ф cos ф + (n-1) ʃsen^n-2 ф d ф
I =-1/n sen^n-1ф cos ф + (n-1)/n ʃ sen^n-2 ф d ф è LEY DE RECURRENCIA MATEMATICA

Ejercicio: dada la ley de recurrencia matemática; calcular la siguiente integral

I = ʃsen5 ф d ф
I = -1/nsen^n-1ф cos ф + (n-1)/n ʃsen^n-2 ф d ф

APLICAR PARA:n = 5

REEMPLAZAMOS: I = -1/5 sen4ф cos ф + 4/5 ʃ sen3 ф d ф è VOLVEMOS: APLICAMOS LA LEY DE
RECUPERANCIA MATEMATICA
I = -1/5 sen4ф cos ф + 4/5[-1/3 sen2ф cos ф +2/3 ʃsen ф d ф]
I = -1/5 sen4ф cos ф - 4/15 sen2ф cos ф – 8/15 cos ф +c

EJERCICIO:
I = ʃsen6 ф d ф = ??
LEY DE RECURRENCIA MATEMATICA: I = -1/n sen^n-1ф cos ф + (n-1)/n ʃ sen^n-2 ф d ф
APLICAR PARA: n=6
Resultado: I = -1/6 sen5ф cos ф + 5/6 ʃsen4 ф d ф
I = -1/6 sen5ф cos ф + 4/6[-1/4 sen3ф cos ф +3/4 ʃsen2 ф d ф]
I = -1/6 sen5ф cos ф - 5/24 sen3ф cos ф +15/28 ʃ sen2 ф d ф
I = -1/6 sen5ф cos ф - 5/24 sen3 ф cos ф +5/8 [-1/2 senф cos ф +1/2 ʃd ф]
I = -1/6 sen5ф cos ф - 5/24 sen3 ф cos ф - 5/16 senф cos ф +5/6 ф + c

EJERCICIOS:
1.- I = ʃ cos5 ф d ф = ??
I = 1/5 cos4ф sen ф + 4/5 ʃ cos3 ф d ф
I = 1/5 cos4ф sen ф + 4/5 [1/3 cos2ф sen ф +2/3 ʃ cos ф d ф]
I = 1/5 cos4ф sen ф + 4/15 cos2 ф sen ф +8/15 senф + c

2.- I = ʃ cos6 ф d ф = ??
I = 1/6 cos5ф sen ф + 5/6 ʃ cos4 ф d ф
I = 1/6 cos5ф sen ф + 5/6 [1/4 cos3ф sen ф +3/4 ʃ cos2 ф d ф]
I = 1/6 cos5ф sen ф + 5/24 cos3 ф sen ф + 15/24 ʃ cos2 ф d ф
I = 1/6 cos5ф sen ф + 5/24 cos3 ф sen ф +15/24 [1/2 cos ф sen ф + 1/2 ʃ d ф]
I = 1/6 cos5ф sen ф + 5/24 cos3 ф sen ф +15/48 cos ф sen ф + 15/48 ф + c

SOLUCION DE DIFERENCIALES QUE CONTIENEN PARAMETROS ESPECIALES
I = ʃex sen x dx
I = ʃ ex sen x dx = uv - ʃ vdu
u = ex dv = sen x dx
du = exdx ʃ dv = ʃ senxdx
v = -cosx
I =-excosx + ʃex cos x dx (a)
I1

· Calculo de I1:

I = ʃ e^x cos x dx = uv - ʃ vdu
u = e^x dv = sen x dx
du = e^xdx ʃ dv = ʃ senxdx
v = senx
I1 =e^x . senx - ʃe^x sen x dx
I1 = e^x . senx – I (b)

Reemplazamos (b) en (a)

I= - e^x cosx + e^x sen x – I
2I= - e^x cosx + e^x sen x
I = 1/2 e^x sen x - 1/2 e^x cosx

2) I
ʃ x^2cosxdx uv- ʃ vdu

u = x^2 dv = cosxdx
du = 2xdx ʃ dv = ʃcosxdx
v = sinx

I = x^2 sin x - ʃ sin x 2x dx
I = x^2 sin x - 2 ʃx sin x dx
I = ʃx sin x dx

u= x dv = sin x
du=dx ʃ dv = ʃ sin x
v = - cos x

I = -x cos x + ʃ cos x dx

I = -x cos x + sin x

I = x^2 sin x + 2 x cos x - 2 sin x + C
I = x^2 sin x + 2 ( x cos x - sin x ) + C

CALCULO DE DIFERENCIAS QUE CONTIENEN LOGARITMOS NATURALES
Ejemplo: I = ʃ x ln x dx

solucion adecuada:

I = ʃ x ln x dx = uv - ʃ vduu = ln x dv = x dxdu = dx/x ʃ dv = ʃ x dxv = x^2/2I = x^2/2 ln x - ʃ x^2/2 dx/x I = x^2/2 ln x - 1/2 ʃ x dxI = x^2/2 ln x - 1/2 x^2/2 + CI = 1/2 x^2 ( ln x -1/2 ) + C
SOLUCION DE DIFERENCIALES QUE CONTIENEN FUNCIONES TRIGONOMETRICAS INVERSA
ejemplo:
I = ʃ Arc sin x dx
solucion:
I = ʃ Arc sin x dx = uv - ʃ vdu
u = Arc sin x dv = dx
du = dx / ( 1 - x^2 )^1/2 ʃ dv = ʃ dx
v = x
I = x Arc sin x -ʃ x dx / ( 1 - x^2 )^1/2
I = x Arc sin x - ʃ x ( 1 - x^2 )^-1/2 dx
I = x Arc sin x + 1/2 ʃ ( 1 - x^2 )^-1/2 (-2x) dx
I = x Arc sin x + 1/2 * ( 1 - x^2 )^-1/2 / 1/2
I = x Arc sin x + ( 1 - x^2 )^1/2 + C

---

DERIVADAS DE LAS FUNCIONES TRIGONOMÉTRICAS INVERSASu = f (x) → du/dx

N°	FUNCION	DERIVADA
	Y = Arc sin u	dy/dx= du/dx / (1- u^2)^1/2
	Y = Arc cos u	dy/dx= - du/dx / (1- u^2)^1/2
03	Y = Arc tan u	dy/dx= du/dx / 1+ u^2
04	Y = Arc cot u	dy/dx= - du/dx / 1+ u^2
05	Y = Arc sec u	dy/dx= du/dx / u( u^2 - 1)^1/2
06	Y = Arc csc u	dy/dx= - du/dx / u( u^2 - 1^1/2

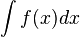http://analisisfigempa.wikispaces.com/Integral+indefinida